Hình đa diện là một dạng hình học không gian ba chiều được giới hạn bởi các đa giác phẳng. Việc xác định số mặt của một hình đa diện là một bài toán cơ bản trong hình học không gian. Bài viết này sẽ hướng dẫn bạn cách xác định số mặt của hình đa diện một cách đơn giản và chính xác.
Mở đầu
Đối với học sinh, sinh viên, đặc biệt là những bạn đang ôn thi đại học, việc làm quen với các dạng bài tập hình học không gian là rất cần thiết. Xác định số mặt của hình đa diện là một trong những dạng bài tập cơ bản, giúp bạn nắm vững kiến thức về hình học không gian và phát triển khả năng tư duy hình học.
Các Bước Xác Định Số Mặt Của Hình Đa Diện
Để xác định số mặt của một hình đa diện, bạn có thể thực hiện theo các bước sau:
- Quan sát hình vẽ: Quan sát kỹ hình đa diện được cho trong đề bài hoặc hình vẽ.
- Phân tích hình dạng: Phân tích hình dạng của hình đa diện, xác định các đa giác phẳng tạo nên hình đa diện đó.
- Đếm số đa giác: Đếm số lượng đa giác phẳng mà bạn đã xác định được ở bước 2.
- Kết luận: Số lượng đa giác phẳng chính là số mặt của hình đa diện.
Ví Dụ Minh Họa
Để hiểu rõ hơn về cách xác định số mặt của hình đa diện, chúng ta cùng xem xét ví dụ sau:
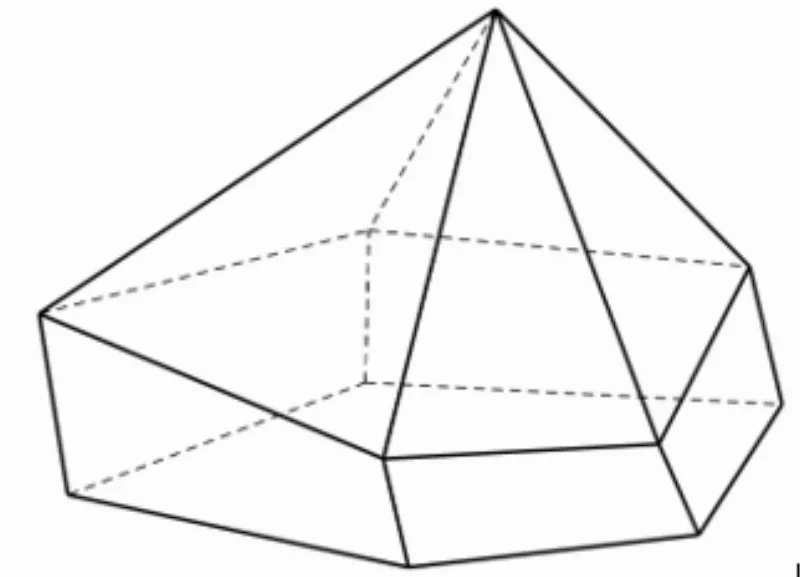
Hình đa diện trong hình vẽ có bao nhiêu mặt?
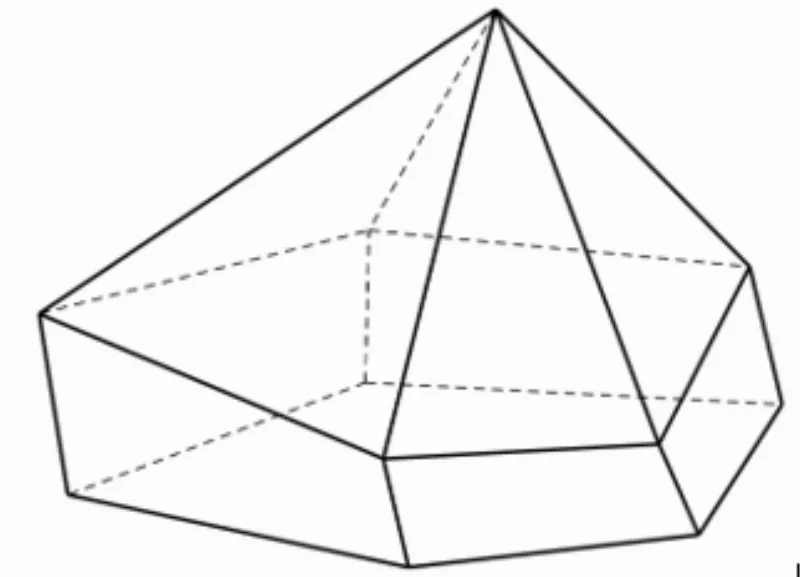 Hình đa diện
Hình đa diện
Phân tích:
- Quan sát: Quan sát hình đa diện, ta thấy hình này được tạo bởi các hình chữ nhật và hình tam giác.
- Phân tích: Hình đa diện bao gồm:
- 2 mặt đáy là hình chữ nhật.
- 4 mặt bên là hình chữ nhật.
- 2 mặt bên là hình tam giác.
- Đếm: Tổng cộng có 2 + 4 + 2 = 8 mặt.
- Kết luận: Hình đa diện trong hình vẽ có 8 mặt.
Lưu ý
- Nên sử dụng bút chì để đánh dấu các mặt đã đếm, tránh việc bỏ sót hoặc đếm trùng lặp.
- Đối với những hình đa diện phức tạp, có thể chia nhỏ hình thành các khối đa diện đơn giản hơn để dễ dàng xác định số mặt.
Bài Tập Vận Dụng
Để củng cố kiến thức, bạn đọc có thể thử sức với bài tập sau:
Xác định số mặt của hình lập phương.
Kết luận
Việc xác định số mặt của hình đa diện là một bài toán cơ bản nhưng rất quan trọng trong hình học không gian. Hy vọng bài viết đã cung cấp cho bạn đọc những kiến thức bổ ích và dễ hiểu về cách giải quyết dạng bài tập này.
Để tìm hiểu thêm về các dạng bài tập hình học không gian khác, bạn đọc có thể tham khảo bài viết về thể tích của khối lập phương.